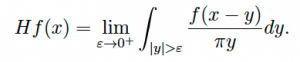A Century of Harmonic Analysis
Lecturers
Professor Anthony Dooley, University of Technology Sydney
Associate Professor Po-Lam Yung, Australian National University
Synopsis
The Fourier transform is an ubiquitous tool that allows one to represent a function as superposition of different frequencies. Its analysis led to substantial progress in the study of partial differential equations and analytic number theory, and has found important applications in diverse fields such as information theory and physics.
One early connection came from the Hilbert Transform:
This is of great interest from many points of view, from complex analysis to boundary value problems for the Laplacian and signal processing (this last connection comes from the formula
a mechanism with which one can can switch on/off a signal). In 1928, Riesz proved that H is bounded onLp(R) for all 1 < p < ∞. This is the beginning of a rich and fruitful theory of singular integrals,concerning operators whose kernels (such as 1/y) barely fails to be integrable on the domain (R in this case). It provides the technical tool required for obtaining a Fourier representation of a general Lp function on R.
Course Overview
- In the first two weeks of this course, we will start with the basics about the Fourier transform on Rn, and study singular integrals such as the Hilbert transform.
- In the last two weeks we will discuss some more advanced topics, such as Bochner-Riesz means (related to the Fourier representation of a general Lp function in Rn when n ≥ 2), the related Fefferman’s disc multiplier, applications to ergodic theory, fractional calculus, and the latest advances in Fourier decoupling inequalities that resolved the main conjecture in Vinogradov’s mean-value theorem in number theory (2015).
Prerequisites
This advanced course will require familiarity with calculus (working knowledge of complex-valued functions with more than one real variable, such as the exponentials of such functions), linear algebra and elementary analysis (involving ϵ’s and δ’s), ideally allied with some Fourier theory and measure theory. This course is aimed at someone who has done the third or fourth year of a mathematics degree, and who is interested in furthering their knowledge of modern analysis.
Assessment
- 2 Assignments (25% each)
- Take-home final (50%)
(may be subject to change)
Attendance requirements
Participation in all lectures and tutorials is expected.
For those completing the subject for their own knowledge/interest, evidence of at least 80% attendance at lectures and tutorials is required to receive a certificate of attendance.
Resources/pre-reading
You are expected to have taken a course on elementary analysis, at the level of W. Rudin’s “Principles of Mathematical Analysis”, and it will be helpful for you to have read:
Not sure if you should sign up for this course?
Take this QUIZ to self-evaluate and get a measure of the key foundational knowledge required.
Professor Anthony Dooley, University of Technology Sydney
Anthony Dooley took up the position of Head of the School of Mathematical and Physical Sciences at UTS in January 2016, following a period of 4 years as Professor of Mathematics at the University of Bath, UK, where he was Deputy Head of Department and the inaugural Director of the Bath Institute for Mathematical Innovation. Before that, he was Professor of Mathematics at UNSW, where he was Head of School of Mathematic s and Statistics, Chair of the Academic Board and Associate Dean (Strategy). His research is in the area of Modern Analysis, including harmonic analysis and dynamical systems.
Associate Professor Po-Lam Yung, Australian National University
Po-Lam Yung is an Associate Professor / Future Fellow at the Australian National University. He received his PhD from Princeton University in 2010, and has since spent time in Rutgers, the State University of New Jersey, the University of Oxford, and the Chinese University of Hong Kong. His research is in the areas of harmonic analysis and partial differential equations.